This question popped up in my mind one fine day, and I couldn’t stop thinking about it. So here’s a blog post about it.

Find all $n \geq 3$ such that $n$ points can be chosen in a 2D integer lattice to form a regular $n$-gon.

Okay, let us unpack what this is asking.

• A lattice refers to the subset of points in $\mathbb{R}^d$ where the coordinates are integer values¹. In particular, a 2D integer lattice is the subset of points $(x,y)$ in $\mathbb{R}^2$ such that $x$ and $y$ are both integers.
• A regular $n$-gon refers to a polygon of $n$ sides (e.g., triangle, rectangle, pentagon) whose sides are of equal length and all internal angles are of equal measure. Common examples of regular $n$-gons are equilateral triangles and squares.

So we are asking for all values of $n \geq 3$ such that the points $(x_1,y_1)$, $(x_2,y_2)$, …, $(x_n, y_n)$ form a regular $n$-gon, where each of the coordinates are integers.

There is an obvious value of $n$ for which this applies: $n = 4$, the case for which our polygon is a square. There are in fact an infinite number of squares that meet our requirement above. But the challenge is to find other values of $n$ that work (if they exist).

Another subtle challenge is that there are multiple orientations to consider when drawing the polygons. Just because a polygon doesn’t work for one orientation doesn’t mean that we can’t find any if the shape is rotated.

To deal with these challenges at the same time, let us consider how the points are located for a regular $n$-gon.

As discussed above, an $n$-gon consists of $n$ sides of equal length and $n$ internal angles which are of equal measure. But consider what this means for the vertices of the $n$-gon — because the $n$ internal angles are of equal measure, that means that the angle between each of the $n$ points must be the same. Since there are $2\pi$ radians ($360^\circ$ degrees) in a full revolution, thus each angle between the points must be $\frac{2\pi}{n}$ radians.

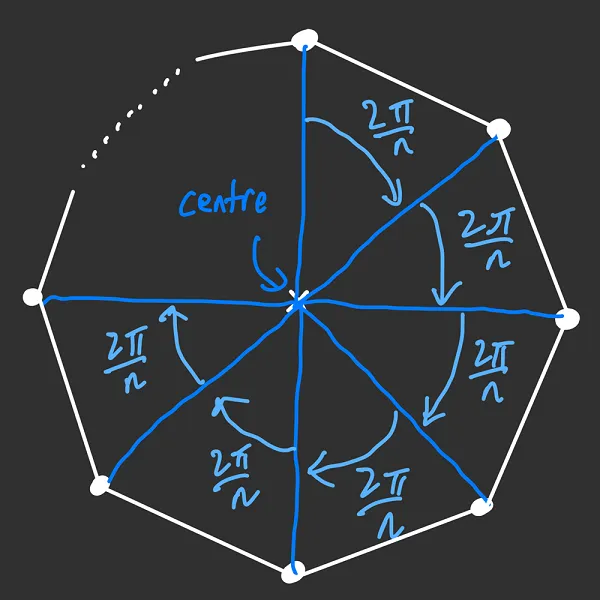
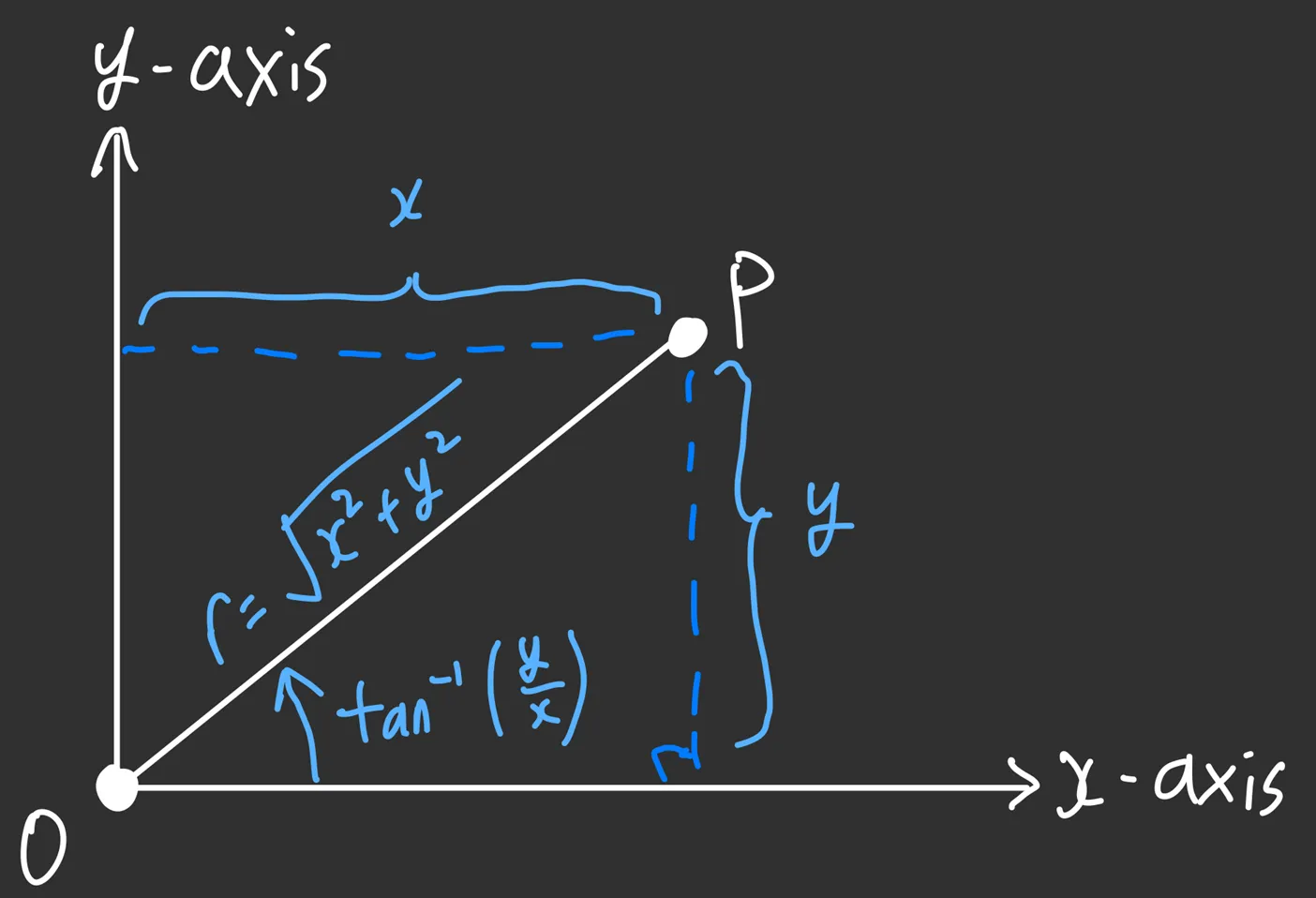
Now let us think about how we can ‘move’ from one point to another on an $n$-gon. More generally, how do we rotate a point in the 2D plane by $\alpha$ radians about the centre (i.e., origin)? We will use the idea of polar coordinates to help us with this. Instead of writing the coordinates of a point using $x$ and $y$, we will specify the distance from the origin, typically denoted $r$ (for the radius of the circle that the point lies on) and the angle between the positive $x$-axis and the point, typically denoted $\theta$.

Suppose a point has the coordinates $(x,y)$. By the Pythagorean theorem, the distance from the origin is $r=\sqrt{x^2+y^2}$. Using trigonometry, one also sees that the angle made between the positive $x$-axis and the point is $\theta=\tan^{-1}\left(\frac yx\right)$². To convert polar coordinates back to Cartesian coordinates, one can simply use the formulae $x = r\cos\theta$ and $y=r\sin\theta$.

So what happens when we rotate a point by an angle $\alpha$ about the origin? The point is still a distance $r$ from the origin, but the angle between the positive $x$-axis and the point is now $\theta+\alpha$. In Cartesian coordinates, the point will have the new coordinates $x' = r\cos(\theta+\alpha)$ and $y' = r\sin(\theta+\alpha)$. Using the angle addition formulae for sine and cosine, we see that

So, rotating a point $P(x,y)$ about the origin by $\alpha$ will result in the point $P'$ with coordinates $(x\cos\alpha - y\sin\alpha, x\sin\alpha + y\cos\alpha)$³.

Back in our original problem, to ‘move’ from one point to another means to rotate that point by a multiple of $\frac{2\pi}n$. So, starting from a point $(x,y)$ on the regular $n$-gon, another point on that $n$-gon must be

where $k \in \{1,2,\dots,n-1\}$.

As we will soon see, this will lead to a problem if we want all points to have integer coordinates.

The challenge lies in making sine and cosine rational. Before we reveal what the core result is, let us examine a lemma.

Lemma. There exists a polynomial $F_n(x)$ such that

$$F_n(2\cos t) = 2\cos nt$$

for all $n \geq 1$, where the degree of $F_n(x)$ is $n$ and $F_n(x)$ is a monic polynomial (i.e., the leading coefficient is 1) with integer coefficients.

This claim is readily proven using mathematical induction on $n$. Let us first cover two base cases. For $n=1$, note that the polynomial $F_1(x) = x$ clearly works. For $n = 2$, we note that the polynomial $F_2(x) = x^2 - 2$ works because

Now let’s assume that the lemma holds for $k$ and $k + 1$ for some $k \geq 1$. We will show that the lemma holds for the $k+2$ case. Observe that, by the sum of cosines formula, we get

which means

and therefore

Hence,

works, with $F_{k+2}(x)$ having degree $k+2$. Also, the leading coefficient of $F_{k+2}(x)$ is the same as the leading coefficient of $F_{k+1}(x)$, which is, by assumption, 1. Therefore, by induction, the lemma is proven. ∎

With this lemma we can prove the main result.

Theorem. The only values of $\theta$, where $0 \leq \theta \leq \frac\pi2$, such that both $\frac\theta\pi$ and $\cos\theta$ are rational are $\theta = 0$ (and $\cos\theta = 1$), $\theta = \frac\pi3$ (and $\cos\theta = \frac12$), and $\theta = \frac\pi2$ (and $\cos\theta = 0$).

This result is quite surprising, but the proof is not too complicated. Suppose $\frac\theta\pi$ is rational, so we can write $\theta = \frac{2\pi k}{n}$ where $k$ and $n$ are both integers⁴ with $n \geq 1$. Suppose $c = 2\cos\theta$ is rational. By the lemma, we observe that

which means that $c$ is a root of $F_n(x) - 2$. Since $c$ is rational, and $F_n(x) - 2$ is a monic polynomial with integer coefficients, thus the Rational Root Theorem tells us that $c$ must be an integer.

However, note that $|c| = |2\cos\theta| \leq 2$ since $-1 \leq \cos \theta \leq 1$. Therefore, the only possible values that $c$ can take are -2, -1, 0, 1, and 2. Thus one must conclude that $\cos \theta \in \{-1,-\frac12,0,\frac12,1\}$. Given that $\theta$ is between $0$ and $\frac\pi2$ inclusive, this means that $\cos\theta \in \{0, \frac12, 1\}$ with $\theta \in \{0, \frac\pi3, \frac\pi2\}$. ∎

One might deduce the following corollary from the above theorem, often called Niven’s Theorem⁵.

Corollary. The only values of $\theta$, where $0 \leq \theta \leq \frac\pi2$, such that both $\frac\theta\pi$ and $\sin\theta$ are rational are $\theta = 0$ (and $\sin\theta = 0$), $\theta = \frac\pi6$ (and $\sin\theta = \frac12$), and $\theta = \frac\pi2$ (and $\sin\theta = 1$).

The proof is quite simple. Let $\alpha = \frac\pi2 - \theta$, so $0 \leq \alpha \leq \frac\pi2$. By the theorem above we know that $\cos(\alpha) = \cos\left(\frac\pi2 - \theta\right) = \sin\theta$ is rational only when $\alpha = 0$ (which means $\theta = \frac\pi2$), $\alpha = \frac\pi3$ (which means $\theta=\frac\pi6$), or $\alpha=\frac\pi2$ (which means $\theta=0$). Consequently the values of $\sin\theta$ that are rational are $0$, $\frac12$, and $1$. ∎

Returning to our problem, what does this theorem tell us? Recall that if a point $(x,y)$ lies on the $n$-gon, then

is another point on the $n$-gon. We also want all the points on the $n$-gon to be integers, which means that both $x\cos\left(\frac{2k\pi}n\right) - y\sin\left(\frac{2k\pi}n\right)$ and $x\sin\left(\frac{2k\pi}n\right) + y\cos\left(\frac{2k\pi}n\right)$ need to be integers. Let us just focus on $x\sin\left(\frac{2k\pi}n\right) + y\cos\left(\frac{2k\pi}n\right)$. We know two things.

• By the above theorem, $\cos\left(\frac{2k\pi}n\right)$ can only be rational when $\frac{2k\pi}n = 0$ (which is impossible since $k \geq 1$), $\frac{2k\pi}n = \frac\pi3$, or $\frac{2k\pi}n = \frac\pi2$.
• By the above corollary (Niven’s Theorem), $\sin\left(\frac{2k\pi}n\right)$ can only be rational when $\frac{2k\pi}n = 0$ (again, impossible since $k \geq 1$), $\frac{2k\pi}n = \frac\pi6$, or $\frac{2k\pi}n = \frac\pi2$.

Thus, for $x\sin\left(\frac{2k\pi}n\right) + y\cos\left(\frac{2k\pi}n\right)$ to be rational, we must have $\frac{2k\pi}n = \frac\pi2$. Regardless of the value of $n$, we need consecutive points on the $n$-gon to work, i.e. the case of $k = 1$ needs to work. For that case we have $\frac{2\pi}n = \frac\pi2$ which means that $n = 4$, i.e. a square.

In conclusion: the only $n$ (where $n \geq 3$) such that $n$ points can be chosen in a 2D integer lattice to form a regular $n$-gon is $n = 4$, which is the (boring) case of the square.

Cover image by D koi on Unsplash. Cropped from the original.